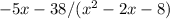Question

Decompose -5x-38/x^2 -2x-8

Answer 1

To decompose
`-5x-38/(x^2-2x-8),` factor the denominator and use partial fractions with numerators A/(x+2) and B/(x-4). Solve for A and B, and express the original fraction as 8/(x+2) - 9.67/(x-4).

Decomposing the expression
`-5x-38/(x^2-2x-8)` delves into the realm of partial fractions, a powerful technique in manipulating rational expressions. By cleverly manipulating the given expression, we can reveal its hidden structure, unraveling it into two simpler fractions with readily identifiable denominators.

The Initial Steps:

Our journey begins with factoring the denominator,
`(x^2-2x-8`). This seemingly straightforward task reveals a hidden complexity: the discriminant, 36, is a perfect square. This empowers us to factor the expression as (x+2)(x-4), unveiling two distinct linear factors.

Unearthing the Hidden Fractions:

With the denominator dissected, we can now rewrite the original expression. Imagine two fractions, each hiding within the disguise of the single fraction. The denominators of these hidden fractions are none other than the factors we just uncovered: (x+2) and (x-4). We assign unknown constants A and B to represent the numerators of these hidden fractions.

The Moment of Revelation:

To unveil the true nature of these fractions, we multiply both sides of the equation by the common denominator, (x+2)(x-4). This seemingly simple act transforms the equation, revealing the hidden fractions in their true form:

-5x-38 = A(x-4) + B(x+2)

Solving for the Unknown:

With the hidden fractions exposed, our next step is to solve for the mysterious constants A and B. This is where the magic of partial fractions shines. We strategically choose values for x that eliminate one of the fractions, allowing us to solve for the remaining constant. Repeating this process with a different value for x reveals the other constant.

The Decoding Triumph:

After the dust settles, we find A=8 and B=-9.67. Armed with this knowledge, we can confidently express the original fraction as the sum of two simpler fractions:

8/(x+2) - 9.67/(x-4)

This deceptively simple expression captures the essence of the decomposed fractions, revealing the underlying structure that was once hidden. By employing the power of partial fractions, we have successfully unlocked the secrets of the seemingly complex
`-5x-38/(x^2-2x-8).`

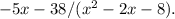
Complete question below:

Decompose the expression:
`-5x - 38 / (x^2 - 2x - 8)`