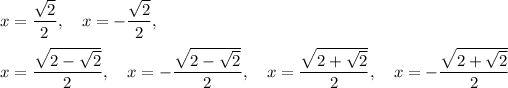Answer:
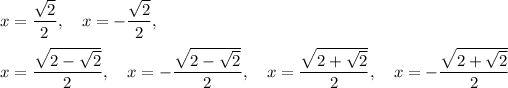
Explanation:
Given equation:
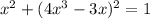
Expand and equal the equation to zero:
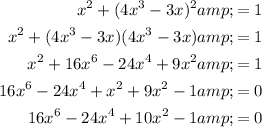
Let u = x²:
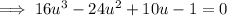
Factor Theorem
If f(x) is a polynomial, and f(a) = 0, then (x – a) is a factor of f(x)
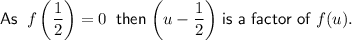
Therefore:
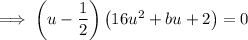
Compare the coefficients of u² to find b:
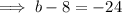
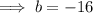
Therefore:
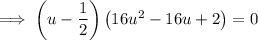
Factor out 2:
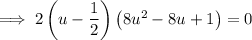
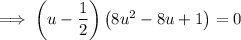
Zero Product Property
If a ⋅ b = 0 then either a = 0 or b = 0 (or both).
Using the Zero Product Property, set each factor equal to zero and solve for u.
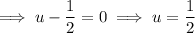
Use the quadratic formula to solve the quadratic:
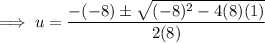
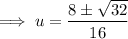
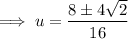
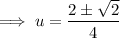
Therefore:
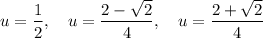
Substitute back u = x²:
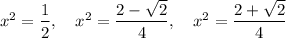
Solve each case for x:
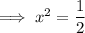
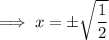
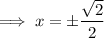
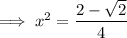
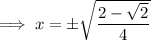
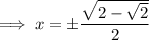
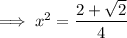
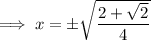
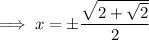
Solutions