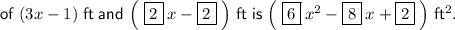Question

Use the model of the rectangular prism to answer the question. The width of the

prism is (2x - 2) ft, and its height is (x + 7) ft. The area of the base of the prism is
(3x2 + 3x - 4) ft².

Could the length of b be (3x - 1) ft? Complete the explanation.

Answer 1

`\textsf{$\boxed{\sf No}$\;. The area of the bottom face of the prism is $(3x^2+3x-4)\; \sf ft^2$, and the product}`

`\textsf{of $(3x-1)$\;ft\;and $\left(\; \boxed{2}\:x-\boxed{2}\;\right)$ ft\;is\;$\left(\; \boxed{6}\:x^2-\boxed{8}\:x+\boxed{2}\;\right)$\;ft$^2$.}`

Explanation:

Given dimensions of a rectangular prism:

• Width = (2x - 2) ft
• Height = (x + 7) ft
• Area of the base = (3x² + 3x - 4) ft²

The area of the base of a rectangular prism is the product of the width of the base and the length of the base.

To determine if length b could be (3x - 1) ft, multiply b by the width of the base of the prism.

`\begin{aligned}\implies \sf Area\;of\;base&=\sf length * width\\&=b * (2x-2)\\&=(3x-1)(2x-2)\\&=3x(2x-2)-1(2x-2)\\&=6x^2-6x-2x+2\\&=6x^2-8x+2\end{aligned}`

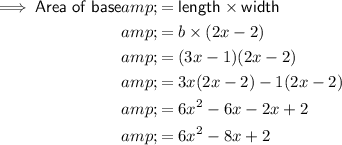
Therefore, the length of b cannot be (3x - 1) as the area of the base when b is (3x - 1) is not equal to the given area of the base.

`\textsf{$\boxed{\sf No}$\;. The area of the bottom face of the prism is $(3x^2+3x-4)\; \sf ft^2$, and the product}`

`\textsf{of $(3x-1)$\;ft\;and $\left(\; \boxed{2}\:x-\boxed{2}\;\right)$ ft\;is\;$\left(\; \boxed{6}\:x^2-\boxed{8}\:x+\boxed{2}\;\right)$\;ft$^2$.}`