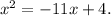Final answer:
The solutions of x² = -11x + 4 are 0.377 and 10.377
None of the given options is correct
Step-by-step explanation:
To find the solutions of the equation
 , we can use the quadratic formula. The quadratic formula states that for an equation in the form
, we can use the quadratic formula. The quadratic formula states that for an equation in the form
 , the solutions for
, the solutions for
 are given by:
are given by:
![\[x = (-b \pm √(b^2 - 4ac))/(2a)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/2zpf361dwzb9cjm28q0mbe26oyvsac2zk9.png)
Comparing the given equation
 with the standard form
with the standard form
 , we have
, we have
 , and
, and

Substituting these values into the quadratic formula, we get:
![\[x = (-(-11) \pm √((-11)^2 - 4(1)(4)))/(2(1))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bw7nhaz7vlbhnx1998b4spt1j4ppy3kbgi.png)
Simplifying this equation further:
![\[x = (11 \pm √(121 - 16))/(2)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/cxaye61u818wavrc56wzx79f0xawdaogck.png)
![\[x = (11 \pm √(105))/(2)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/45h050rok642x4jlvl849426mrtlakf04r.png)
Now, let's calculate the value of
 :
:
![\[√(105) \approx 10.246\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/x22u1lj8gy1g0xyswv9icvbbavn7zp0jwe.png)
So, the solutions for x are:
![\[x = (11 \pm 10.246)/(2)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/iolzvcaxwqqil2vccr2hreor3i0i6zbv3d.png)
![\\\[x_1 \approx (11 - 10.246)/(2) \approx 0.377\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/x140j41458o4ty10drl4f955ets3tqq0nv.png)
![\[x_2 \approx (11 + 10.246)/(2) \approx 10.377\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/zl5dndgt2jb478bx1r06uhm97vi2xxldoy.png)
Therefore, none of the given options (a, b, c, d) matches the correct solutions for the equation