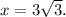Question

Someone who’s good at logs please help lol

Answer 1

To three significant figures, the value of 3 log47 is approximately 7.984. The solution to the equation
`\(\log_3{x} = (1)/(log_27(x))\)` is
`\(x = 3√(3)\).`

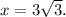
To convert 3 log47 to base e, we can use the change of base formula:

loga(x) = logb(x) / logb(a)

In this case, a = 47, b = e, and x = 3. So, we have:

3 log47 = 3 loge(474) / loge(10)

Using a calculator, we can find that loge(474) ≈ 6.160, and loge(10) ≈ 2.303. Plugging these values into the equation, we get:

3 log47 ≈ 3 * 6.160 / 2.303 ≈ 7.984

So, to three significant figures, the value of 3 log47 is approximately 7.984.

For the second question:

To solve the equation
`\(\log_3{x} = (1)/(log_27(x))\)`, let's first simplify the expression on the right side.

Recall that
`\(log_a^n(b) = (1)/(n) \log_a{b}\)`. Applying this property to
`\(log_27(x)\)`, we get:

`\((1)/(log_27(x)) = \frac{1}{(1)/(3)\log_3{x}}\)`.

Now, let's substitute this into the original equation:

`\(\log_3{x} = \frac{1}{(1)/(3)\log_3{x}}\)`.

To get rid of the fraction in the denominator, multiply both sides by
`\((1)/(3)\log_3{x}\)`:

`\((1)/(3)\log_3{x} \cdot \log_3{x} = 1\)`.

Now, solve for
`\(\log_3{x}\)`:

`\(\log_3{x} \cdot (1)/(3)\log_3{x} = 1\)`.

Multiply both sides by 3:

`\(\log_3{x} \cdot \log_3{x} = 3\)`.

Simplify the left side:

`\(\log_3{x^2} = 3\)`.

Now, exponentiate both sides:

`\(x^2 = 3^3\)`.

`\(x^2 = 27\)`.

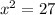Now, take the square root of both sides (since we're looking for a positive value of x):

`\(x = √(27)\)`.

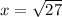Simplify:

`\(x = 3√(3)\)`.

So, the solution to the equation is
`\(x = 3√(3)\).`