Question

Find g(x) if g'(x)=-2g(x) and g(0)=5?

Answer 1

Main Answer:

The solution,
`g(x) = 5e^(-2x),` satisfies g
`'(x) = -2g(x)` with the initial condition
`g(0) = 5,` exhibiting exponential decay.
`g(x) = 5e^(-2x)`.

Step-by-step explanation:

The solution to the given differential equation
`g'(x) = -2g(x)`with the initial condition
`g(0) = 5 is g(x) = 5e^(-2x).` This is obtained by recognizing the form of the solution for a first-order linear homogeneous differential equation, where the derivative of the function is proportional to the function itself with a constant factor. The solution involves the exponential function with the constant factor
`(-2)`determining the rate of decay.

In this specific case, the initial condition
`g(0) = 5` allows us to determine the value of the arbitrary constant in the general solution. Substituting
`x = 0` into the equation, we get
`5 = 5e^(0)`, resulting in the constant term being 1. Thus, the particular solution to the initial value problem is
`g(x) = 5e^(-2x).`

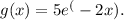
This exponential function describes a decay process where the function approaches zero as x increases. The negative exponent indicates the decay, and the initial value determines the starting point of this decay process. In summary, the solution
`g(x) = 5e^(-2x)`satisfies the given differential equation with the specified initial condition.