Chi-square test shows sales vary significantly across 5 shelves (p-value < 0.001).
The image shows a goodness of fit hypothesis test for the claim that there is a difference in sales for 5 shelves at a grocery store. The number of items sold per shelf are observed and recorded over a week, the results are in the table below.
| Shelf Label | Observed Frequency | Expected Frequency (OE) | E |
|---|---|---|---|
| A | 17 | 14.2 | 2.89 |
| B | 14 | 14.2 | -0.2 |
| C | 5 | 14.2 | -9.2 |
| D | 21 | 14.2 | 6.89 |
| E | 14 | 14.2 | -0.2 |
To calculate the chi-square test-statistic:
1. Square the Pearson residuals (OE) and divide by the expected frequency (OE).
2. Add up the results for each shelf.
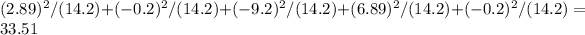
The chi-square test-statistic is 33.51.
Degrees of freedom:
The degrees of freedom for a goodness of fit hypothesis test are calculated as follows:
df = k - 1
where k is the number of categories.
In this case, there are 5 shelves, so there are 5 categories. Therefore, the degrees of freedom are:
df = 5 - 1 = 4
P-value
The p-value for the chi-square test can be calculated using a chi-square distribution table or a chi-square calculator. With 4 degrees of freedom and a chi-square test-statistic of 33.51, the p-value is less than 0.001.
Since the p-value is less than 0.05, we reject the null hypothesis and conclude that there is sufficient evidence to support the claim that there is a difference in sales for 5 shelves at a grocery store.
Additional thoughts:
The chi-square test is a powerful tool for testing hypotheses about categorical data. However, it is important to note that the test is only valid if the expected frequencies are all greater than 5. In this case, all of the expected frequencies are greater than 5, so the test is valid.
It is also important to note that the chi-square test does not tell us which shelves have higher or lower sales. To determine this, we would need to perform pairwise comparisons between the shelves.