Question

College Algebra Question please help!

Answer 1

The equation 16^(2x - 5) = 4^(x + 4) is solved by expressing both sides with a common base (base 2), equating the exponents, and then solving for x to find that x =
`(14)/(3)` or approximately 4.67.

To solve for x in the equation 16^(2x - 5) = 4^(x + 4), we need to recognize that both sides of the equation have bases that are powers of 2 because 16 is
`2^4` and 4 is
`2^2`. This allows us to rewrite the equation with a common base:

(
`2^4`)^(2x - 5) = (
`2^2`)^(x + 4).

Now applying the rule of exponents that states
`(a^b)^c`=
`a^{(bc)`, we get:

2^(4(2x - 5)) = 2^(2(x + 4)).

Since the bases are now the same, we can equate the exponents:

4(2x - 5) = 2(x + 4).

Now, we simply solve for x:

• Distribute the 4 and the 2 to get: 8x - 20 = 2x + 8.
• Subtract 2x from both sides to get: 6x - 20 = 8.
• Add 20 to both sides to get: 6x = 28.
• Finally, divide by 6 to find x: x =
  `(28)/(6)` = 1
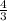  `(4)/(3)` or approximately 4.67.

The solution to the equation is x =
`(14)/(3)` or x ≈ 4.67.