Answer:
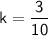
 when
when
 ,
,
 , and
, and
 ,
,
Explanation:
If
 varies jointly as
varies jointly as
 ,
,
 , and
, and
 , the equation of variation is given by:
, the equation of variation is given by:
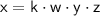
where
 is the constant of variation.
is the constant of variation.
To find the constant
 , substitute the given values
, substitute the given values
 ,
,
 ,
,
 , and
, and
 into the equation:
into the equation:
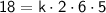
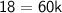
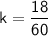
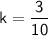
Now that we have the constant of variation
 , we can use it to find
, we can use it to find
 when
when
 ,
,
 , and
, and
 :
:
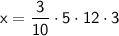
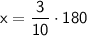

Therefore, when
 ,
,
 , and
, and
 , the value of
, the value of
 is 54.
is 54.