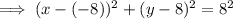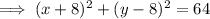Question

NO LINKS!! Please assist me with this problem Part 1m​

Answer 1

`(x+8)^2+(y-8)^2=64`

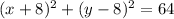
Explanation:

Required conditions:

• Tangent to both axes.
• Center in the second quadrant.
• Radius = 8 units.

If the circle is tangent to both axes, its center will be the same distance from both axes. That distance is its radius.

If the center of the circle is in quadrant II, the center will have a negative x-value and a positive y-value → (-x, y).

Therefore, the coordinates of the center will be (0-r, 0+r) where r is the radius.

If the radius is 8 units, then the center is (-8, 8).

`\boxed{\begin{minipage}{4 cm}\underline{Equation of a circle}\\\\$(x-a)^2+(y-b)^2=r^2$\\\\where:\\ \phantom{ww}$\bullet$ $(a, b)$ is the center. \\ \phantom{ww}$\bullet$ $r$ is the radius.\\\end{minipage}}`

Substitute the found center and given radius into the formula to create an equation for the circle that satisfies the given conditions:

`\implies (x-(-8))^2+(y-8)^2=8^2`

`\implies (x+8)^2+(y-8)^2=64`

Answer 2

• (x + 8)² + (y - 8)² = 64

=======================

Given Conditions

• Tangent to x-axis,
• Tangent to y-axis,
• In the second quadrant,
• Radius is 8 units.

Solution

Equation of circle:

• (x - h)² + (y - k)² = r², where (h, k) is center and r - radius

The center is the radius long distance from the x- axis to left and y-axis up same distance, this makes it in the second quadrant.

So the coordinates of the center are:

• x = - 8, y = 8

The equation is:

• (x - (-8))² + (y - 8)² = 8²
• (x + 8)² + (y - 8)² = 64