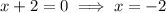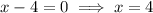Question

Follow the steps to solve the equation.

Answer 1

Given equation is

`\sqrt[3]{x {}^(2) - 7 } = \sqrt[3]{2x + 1}`

to solve this equation we first need to cube both the sides . As this would remove the cube root on both the sides ,

`\longrightarrow (\sqrt[3]{x^2-7})^3 = (\sqrt[3]{2x+1})^3`

This would become ,

`\longrightarrow x^2-7=2x+1 \\`

`\longrightarrow x^2-2x-7-1=0\\`

`\longrightarrow x^2-2x-8=0\\`

`\longrightarrow x^2 -4x +2x -8=0\\`

`\longrightarrow x(x-4)+2(x-4)=0\\`

`\longrightarrow (x+2)(x-4)=0\\`

`\longrightarrow \underline{\underline{ x = 4,-2}}`

And we are done!

Answer 2

`\textsf{To solve the given equation, $\boxed{\sf cube}$ both sides}.`

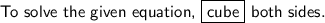
Explanation:

Given equation:

`\sqrt[3]{x^2-7} =\sqrt[3]{2x+1}`

`\textsf{Apply exponent rule} \quad \sqrt[n]{a}=a^{(1)/(n)}:`

`\implies (x^2-7)^{(1)/(3)}=(2x+1)^{(1)/(3)}`

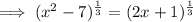
Cube both sides of the equation:

`\implies \left( (x^2-7)^{(1)/(3)}\right)^3= \left((2x+1)^{(1)/(3)}\right)^3`

`\textsf{Apply exponent rule} \quad (a^b)^c=a^(bc):`

`\implies (x^2-7)^{(3)/(3)}=(2x+1)^{(3)/(3)}`

`\implies (x^2-7)^(1)=(2x+1)^(1)`

`\textsf{Apply exponent rule} \quad a^1=a:`

`\implies x^2-7=2x+1`

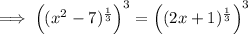
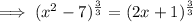
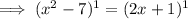
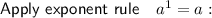
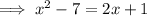
Subtract 2x from both sides:

`\implies x^2-2x-7=1`

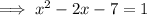
Subtract 1 from both sides:

`\implies x^2-2x-8=0`

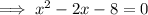
Rewrite -2x as (-4x + 2x):

`\implies x^2-4x+2x-8=0`

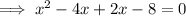
Factor the first two terms and the last two terms separately:

`\implies x(x-4)+2(x-4)=0`

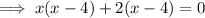
Therefore:

`\implies (x+2)(x-4)=0`

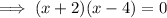
Apply the zero-product property:

`x+2=0 \implies x=-2`

`x-4=0 \implies x=4`