Question

.............................
...................... ......​

Answer 1

a = 20

b = 10

Or if in coordinate format, (20,10)

Explanation:

`\left \{ {{4a-3b=50} \atop {5a-2b=80}} \right.`

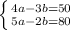
Solve the system using elimination:

In elimination, you want to eliminate a term. I want to eliminate b, so what I would do is to get it the same coefficient (LCM)

• 
  `\left \{ {4a - 3b=50} \atop {5a-2b=80}} \right.`
• 
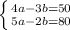
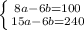  `\left \{ {{8a-6b=100} \atop {15a-6b=240}} \right.` <= Multiply the equations by 3 to find LCM
• 
  `-7a = -140\\` Remember, if the terms you want to eliminate have the same sign in front of them ( - or +), subtract the top equation from the bottom. If they are different signs, add the two equations.
• 
  `a=20`

Now, plug in 20 for an into any of the original equations

• 4a - 3b = 50
• 4(20) - 3b = 50
• 80 - 3b = 50
• -3b = -30
• b = 10

The solution of the system is written as a coordinate, in alphabetical order. Since the variables are a and b, you write it as (a,b).

The solution is
`\boxed{(20,10)}`

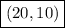
-Chetan K