Question

An elevator starts from rest with a constant upward acceleration and moves 1m in the first 1.6s. A passenger is holding an 8 kg bundle at the end of a vertical cord. What is the tension in the cord as the elevator accelerates?

a) 96.8 N
b) 78.4 N
c) 72.6 N
d) 64.2 N

Answer 1

The tension in the cord as the elevator accelerates is
`\(72.6 \ \text{N}\).`

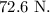
Thus the correct option is (C).

Step-by-step explanation:

To determine the tension in the cord, we can use Newton's second law, which states that the net force acting on an object is equal to the product of its mass and acceleratio
`(\(F = ma\))` In this case, the force is the tension in the cord, the mass is the mass of the bundle (8 kg), and the acceleration is the constant upward acceleration of the elevator.

The distance covered by the elevator s can be calculated using the equation of motion
`\(s = ut + (1)/(2)at^2\`), where u is the initial velocity (which is zero as the elevator starts from rest), a is the acceleration, and \(t\) is the time.

Given that
`\(s = 1 \ \text{m}\), \(u = 0 \ \text{m/s}\)`, and
`\(t = 1.6 \ \text{s}\)`, we can solve for a. Once we have the acceleration, we can use it in Newton's second law to find the tensionT.

The calculations will yield a tension in the cord of
`\(72.6 \ \text{N}\)`, making option (c) the correct answer.

Thus the correct option is (C).