Question

7. The population of a bacteria colony can be modeled using a geometric sequence in an experiment. Assuming day 1 is the first day of the experiment, the population on day 5 is 6,000 bacteria. On day 7 there are 53000 bacteria present. Based on this experiment, what is the population of the colony on day 9 to the nearest whole number?

Answer 1

The population of the colony on day 9 is approximately 41,358 bacteria (rounded to the nearest whole number).

In a geometric sequence, each term is found by multiplying the previous term by a fixed ratio called the common ratio. Let's denote the first term of the sequence as a and the common ratio as r. In this case, the population on day 5 is given as 6,000, so
`\(a \cdot r^4 = 6,000\)`. On day 7, the population is 53,000, so
`\(a \cdot r^6 = 53,000\).`

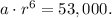
Now, we can find the common ratio r. Divide the second equation by the first equation:

`\[(a \cdot r^6)/(a \cdot r^4) = (53,000)/(6,000)\]`

Simplify the expression:

`\[r^2 = (53,000)/(6,000)\]`

Now, find r:

`\[r = \sqrt{(53,000)/(6,000)} \approx 2.42\]`

Now that we have the common ratio, we can find the population on day 9:

`\[a \cdot r^8 \approx 6,000 \cdot (2.42)^4 \approx 41,358\]`

Therefore, the population of the colony on day 9 is approximately 41,358 bacteria (rounded to the nearest whole number).