Question

NO LINKS!! Please help me with this graph​

Answer 1

`[d(A,C)]^2=\boxed{234}`

`[d(A,B)]^2+[d(B,C)]^2=\boxed{234}`

`\sf Area=\boxed{54}\; units^2`

Step-by-step explanation:

From inspection of the given diagram:

• A = (10, 6)
• B = (1, -3)
• C = (-5, 3)

If ΔABC is a right triangle, the sum of the squares of the two shorter sides will equal the square of the longest side. This is the definition of Pythagoras Theorem.

Use the distance formula to find the length of each side of the triangle.

`\boxed{\begin{minipage}{7.4 cm}\underline{Distance between two points}\\\\$d=√((x_2-x_1)^2+(y_2-y_1)^2)$\\\\\\where $(x_1,y_1)$ and $(x_2,y_2)$ are the two points.\\\end{minipage}}`

`\begin{aligned}d[(A,C)]&=√((x_C-x_A)^2+(y_C-y_A)^2)\\&=√((-5-10)^2+(3-6)^2)\\&=√((-15)^2+(-3)^2)\\&=√(225+9)\\&=√(234)\end{aligned}`

`\begin{aligned}d[(A,B)]&=√((x_B-x_A)^2+(y_B-y_A)^2)\\&=√((1-10)^2+(-3-6)^2)\\&=√((9)^2+(-9)^2)\\&=√(81+81)\\&=√(162)\end{aligned}`

`\begin{aligned}d[(B,C)]&=√((x_C-x_B)^2+(y_C-y_B)^2)\\&=√((-5-1)^2+(3-(-3))^2)\\&=√((-6)^2+(6)^2)\\&=√(36+36)\\&=√(72)\end{aligned}`

Therefore:

• The longest side of the triangle is line segment AC.
• The two shorter sides of the triangle are line segments AB and BC.

`\boxed{\begin{minipage}{9 cm}\underline{Pythagoras Theorem} \\\\$a^2+b^2=c^2$\\\\where:\\ \phantom{ww}$\bullet$ $a$ and $b$ are the legs of the right triangle. \\ \phantom{ww}$\bullet$ $c$ is the hypotenuse (longest side) of the right triangle.\\\end{minipage}}`

Therefore, the triangle is a right triangle if:

`[d(A,B)]^2+[d(B,C)]^2=[d(A,C)]^2`

Substitute the found side lengths into the formula:

`\implies [√(162)]^2+[√(72)]^2=[√(234)]^2`

`\implies162+72=234`

`\implies 234=234`

Hence proving that ΔABC is a right triangle.

To find the area of a right triangle, half the product of the two shorter sides:

`\begin{aligned}\implies \sf Area &= (1)/(2)bh\\&=(1)/(2) \cdot [d(A,B)] \cdot [d(B,C)]\\&=(1)/(2) \cdot √(162) \cdot √(72)\\&=(1)/(2) \cdot √(162 \cdot 72)\\&=(1)/(2) \cdot √(11664)\\&=(1)/(2) \cdot √(108^2)\\&=(1)/(2) \cdot 108\\&=54 \sf \; units^2\end{aligned}`

Answer 2

Answers:

• 1st box = 234
• 2nd box = 234
• 3rd box = 54

=========================================================

Step-by-step explanation:

The three points are at these locations:

• A = (10, 6)
• B = (1,-3)
• C = (-5, 3)

The notation "d(A,C)" means "the distance from A to C". It's equivalent to saying "the length of segment AC".

Then writing
`\left[d(A,C)]^2` means we'll square that distance.

Use the distance formula to get...

`A = (x_1,y_1) = (10,6) \text{ and } C = (x_2, y_2) = (-5,3)\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((10-(-5))^2 + (6-3)^2)\\\\d = √((10+5)^2 + (6-3)^2)\\\\d = √((15)^2 + (3)^2)\\\\d = √(225 + 9)\\\\d = √(234)\\\\`

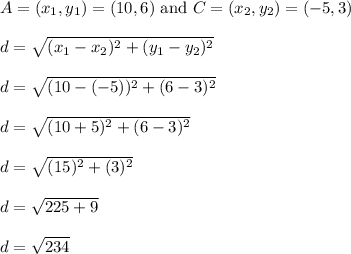
This is the exact length of segment AC. That value squares to 234.

`d = √(234) \ \to \ d^2 = (√(234))^2 = 234\\\\`

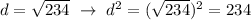
The square root and squaring operation cancel each other out. Think of it like fire vs water.

So we really only care about what's under the square root; rather than the entire square root expression itself. Which is nice because we don't have to worry about pesky things like decimal values.

This is why 234 is typed into the first box.

---------------------

Next, use the distance formula to find how far it is from A to B. Square the result to get what you see below.

`A = (x_1,y_1) = (10,6) \text{ and } B = (x_2, y_2) = (1,-3)\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((10-1)^2 + (6-(-3))^2)\\\\d = √((10-1)^2 + (6+3)^2)\\\\d = √((9)^2 + (9)^2)\\\\d = √(81 + 81)\\\\d = √(162)\\\\d^2 = (√(162))^2\\\\d^2 = 162\\\\`

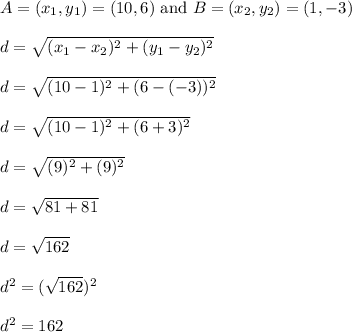
This is the value of
`\left[d(A,B)\right]^2`

Now find the distance from B to C, and square the result.

`B = (x_1,y_1) = (1,-3) \text{ and } C = (x_2, y_2) = (-5,3)\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((1-(-5))^2 + (-3-3)^2)\\\\d = √((1+5)^2 + (-3-3)^2)\\\\d = √((6)^2 + (-6)^2)\\\\d = √(36 + 36)\\\\d = √(72)\\\\d^2 = \left(√(72)\right)^2\\\\d^2 = 72\\\\`

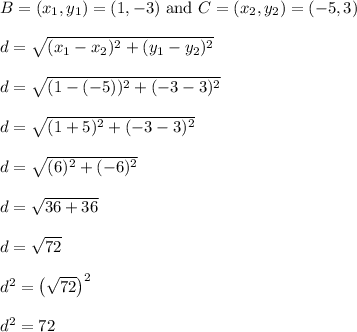
Add this to the previous squared value and we get 162+72 = 234, which matches exactly with the 234 found up toward the top.

We'll write 234 in the 2nd box as well.

This shows that
`\left[d(A,C)\right]^2 = \left[d(A,B)\right]^2+\left[d(B,C)\right]^2` is a true statement. By the converse of the Pythagorean theorem, we have confirmed this is a right triangle.

In other words, we've shown that
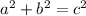`a^2+b^2 = c^2` is a true statement (a,b,c are the sides of the right triangle such that c is the hypotenuse).

---------------------

Recall that we found these segment lengths:

`AB = √(162) = \text{leg1}\\\\BC = √(72) = \text{leg2}\\\\AC = √(234) = \text{hypotenuse}\\\\`

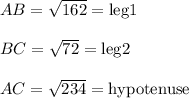
The legs of a right triangle represent the base and height, in either order. This is because the legs are perpendicular to one another. They form a right (aka 90 degree) angle.

`\text{area} = (1)/(2)*\text{base}*\text{height}\\\\\text{area} = (1)/(2)*\text{AB}*\text{BC}\\\\\text{area} = (1)/(2)*√(162)*√(72)\\\\\text{area} = (1)/(2)*√(162*72)\\\\\text{area} = (1)/(2)*√(11664)\\\\\text{area} = (1)/(2)*108\\\\\text{area} = 54\\\\`

Here are some alternative methods you can follow to find the area of this triangle.

• Pick's Theorem
• Shoelace Theorem
• Create a bounding box around the triangle. Make the box as small as possible. Find the area of the whole box, and subtract off the smaller pieces outside the triangle.
• Heron's Formula

As for verifying the answers, you can use a tool like GeoGebra.