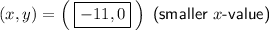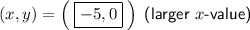Answer:
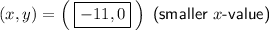
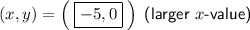
Explanation:

The points that are a distance of 5 units from P(-8, 4) will be all the points on the circumference of a circle with center (-8, 4) and radius 5.
Substitute the center and radius into the formula to create an equation of the circle:
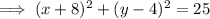
The y-value of any point on the x-axis is zero.
Therefore, to find the points on the x-axis that are 5 units from point P, substitute y = 0 into the equation of the circle and solve for x:
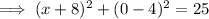
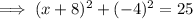
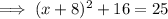
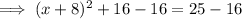
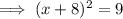
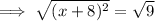
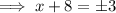
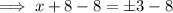

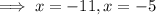
Therefore: