Question

NO LINKS!! Please help me with this symmetry part 3 Select all that apply​

Answer 1

`y=-(1)/(8)x^3`

Explanation:

If a function is symmetrical about the origin, when y is replaced with (-y) and x is replaced with (-x), the resulting function will be equal to the original function.

Original function:

`y=-(1)/(8)x^3`

Replace y with (-y) and x with (-x):

`\implies -y=-(1)/(8)(-x)^3`

`\implies -y=-(1)/(8)\cdot -x^3`

`\implies -y=(1)/(8)x^3`

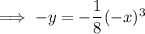
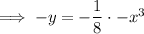
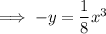
Multiply both sides by -1:

`\implies y=-(1)/(8)x^3`

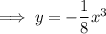
Therefore, as the function is equal to the original function, this function is symmetric with respect to the origin.