Final Answer:
The dimensions of the rectangular garden are 55 feet in length and 40 feet in width.
Step-by-step explanation:
To determine the dimensions of the rectangular garden, let's denote the width as w and the length as
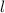 . According to the given information, the length is 15 feet longer than the width, so we can express the length in terms of the width as
. According to the given information, the length is 15 feet longer than the width, so we can express the length in terms of the width as
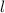 = w + 15. The area (A) of a rectangle is given by the formula A =
= w + 15. The area (A) of a rectangle is given by the formula A =
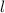 × w.
× w.
Given that the area is 2200 square feet, we can set up the equation:
(w + 15)× w = 2200
Expanding and rearranging the equation:
 + 15w - 2200 = 0
+ 15w - 2200 = 0
Now, we can solve for w using the quadratic formula:
![\[ w = \frac{{-b + \sqrt{{b^2 - 4ac}}}}{2a} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/x4we3vptg3z9bdlyswmh3nk832sywsd0qo.png)
For our equation, a = 1, b = 15, and c = -2200. Plugging in these values:
![\[ w = \frac{{-15 + \sqrt{{15^2 - 4(1)(-2200)}}}}{2(1)} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/nhytm6rw90f7fi158k7i9oipimbtijv2h3.png)
Solving further gives two possible solutions for w , but since the width cannot be negative, we discard the negative solution. Therefore, w = 40 . Now, we can find the length (
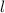 ):
):
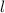 = w + 15 = 40 + 15 = 55
= w + 15 = 40 + 15 = 55
Hence, the dimensions of the rectangular garden are 55 feet in length and 40 feet in width.