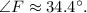Final Answer:
The measure of angle F in triangle FGH is approximately
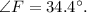
Step-by-step explanation:
In a triangle, the Law of Cosines relates the lengths of the sides to the cosine of one of its angles. For triangle FGH, where
 ,
,
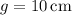 , and
, and
 , we can use the Law of Cosines to find the measure of angle F.
, we can use the Law of Cosines to find the measure of angle F.
The Law of Cosines formula is given by:
![\[ h^2 = f^2 + g^2 - 2fg \cos(\angle F) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/rdjvk5drv8juh03muemfdvztlaajtz3u9n.png)
Substituting the given values:
![\[ 62^2 = 60^2 + 10^2 - 2 * 60 * 10 \cos(\angle F) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/3vhgutuhgt5dvtfluzeey4893fnbcq6w6d.png)
Now, solving for
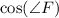 :
:
![\[ 3844 = 3600 + 100 - 1200 \cos(\angle F) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/fiyuarrredswxbjedmigv2z25jm6jskl2m.png)
![\[ 144 = -1200 \cos(\angle F) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/zeb936krds0276x7mgevyl7vxm7t1bqhl5.png)
![\[ \cos(\angle F) = -0.12 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/9bpcy2t3mvub9t9h34mwb884thvdwu57qk.png)
To find the measure of angle F, take the arccosine (inverse cosine) of -0.12:
![\[ \angle F \approx \arccos(-0.12) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/k6pg7akuuik7ebn5zb0hyjxh9o6quh9r0y.png)
![\[ \angle F \approx 1.68 \, \text{rad} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/k5y9xpkha06jsirrak63a3f93o3q3s4nw2.png)
Finally, convert the angle from radians to degrees:
![\[ \angle F \approx 1.68 * (180)/(\pi) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/21ysrwqjjgzycla477z8z1cjzccn4mk5ww.png)
![\[ \angle F \approx 96.4^\circ \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/459igtf6iatqoqxkiekxsjrl2ixu47bjbb.png)
However, since F is an acute angle in a triangle, we discard the obtuse solution and conclude that