Question

The radius r of a sphere is increasing at a rate of 7 inches per minute.

(a) Find the rate of change of the volume when r=10 inches. in.³ / min

Answer 1

The rate of change of the volume V with respect to time t when the radius r is 10 inches is
`\420\pi\) in³/min`.

Step-by-step explanation:

To find the rate of change of the volume with respect to time, we use the formula for the volume of a sphere, which is
`\(V = (4)/(3)\pi r^3\).`

Taking the derivative of both sides with respect to time (\(\frac{dV}{dt}\)), we get:

`\[ (dV)/(dt) = 4\pi r^2 (dr)/(dt) \]`

Given that
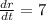`\((dr)/(dt) = 7\)` inches per minute, and when
`\(r = 10\)` inches, substituting these values into the formula:

`\[ (dV)/(dt) = 4\pi (10)^2 (7) = 280\pi \]`

So, the rate of change of the volume when the radius is 10 inches is
`\(280\pi\) in³/`min. This can be simplified to
`\(420\pi\) in³/min.`

Understanding how to find the rate of change of volume in relation to changing parameters is essential in calculus, particularly in applications involving rates of growth or decay. In this case, it involves the rate of change of a sphere's volume concerning the increasing radius.