Question

where is a positive constant and is the acceleration due to gravity, is a model for the velocity of a body of mass that is falling under the influence of gravity. Because the term represents air resistance, the velocity of a body falling from a great height does not increase without bound as time increases. Use a phase portrait of the differential equation to find the limiting, or terminal, velocity of the body. Explain your reasoning.

Answer 1

`v_(T)` =
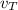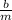`(b)/(m)` g

Step-by-step explanation:

For this exercise we use Newton's second law

∑ F = m a

where they relate it is

a = dv / dt

v = dx / dt

in this case we have two forces: the weight of the body and the friction of the air

fr -W = m a

there are several ways to approximate the friction force in a fluid, if the velocity of the body is low we can use

fr = b v

for high speeds, higher power speed terms are entered

we substitute

b v - m g = m dv / dt

`(dv)/(dt)` =
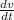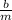`(b)/(m)` v -g

We can see that as the speed increases, we reach the point that the term on the right is zero, at this point there is no acceleration, therefore the speed is constant and is called the terminal velocity.

0 =
`(b)/(m) \ v_T` -g

`v_(T)` =
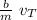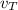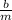`(b)/(m)` g

the constant b is given by the conditions of the air, pressure, density and temperature