Question

Suppose $2000 is invested in an account that pays interest at a 7% annual rate.

a. How much is in the account after 10 years if the interest is compounded annually?
b. How much is in the account after 10 years if the interest is compounded continuously?
c. How long will it take for the value of the investment to double if the interest is compounded annually?
d. How long will it take for the value of the investment to double if the interest is compounded continuously?

Answer 1

After 10 years, $2000 invested at 7% annual interest compounded annually will become approximately $3937.70 and compounded continuously it'll be approximately $4030.23. To double the investment with annual compounding takes approximately 10.24 years, and with continuous compounding, it's approximately 9.90 years.

Step-by-step explanation:

When $2000 is invested in an account with a 7% annual interest rate compounded annually, we use the compound interest formula to determine the amount in the account after 10 years:
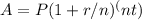`A = P(1 + r/n)^(nt)`. Here, P is the principal amount ($2000), r is the annual interest rate (0.07), n is the number of times interest is compounded per year (1 for annually), t is the number of years (10).

Compound Interest Annually

For part a, substituting our values in we get:
`A = 2000(1 + 0.07/1)^(1*10) = 2000(1.07)^10 = $3937.70` approximately after 10 years.

Compound Interest Continuously

For part b, the formula for continuously compounded interest is A =
`Pe^(rt)`. Substituting our values, we get:
`A = 2000e^(0.07*10) = 2000e^0.7 = $4030.23`approximately after 10 years.

Doubling Time with Annual Compounding

For part c, we need to solve for t in the equation
`P(1 + r/n)^(nt) = 2P`, which gives us
`2000(1.07)^t = 400`0. Using logarithms, t = log(2) / log(1.07) = 10.24 years approximately.

Doubling Time with Continuous Compounding

For part d, we use the continuous compounding formula and solve for t in the equation
`Pe^(rt) = 2P`, which gives us 2000e^(0.07t) = 4000. This simplifies to t = (log(2) / 0.07) = 9.90 years approximately.