Final Answer:
The quadratic polynomial that completes the factorization is
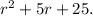
Step-by-step explanation:
To find the quadratic polynomial that completes the factorization of
 , let's first recognize that
, let's first recognize that
 is the difference of cubes, which can be factored as
is the difference of cubes, which can be factored as
 . Here, (r - 5) corresponds to the given factor. Now, we need to determine the quadratic factor.
. Here, (r - 5) corresponds to the given factor. Now, we need to determine the quadratic factor.
The quadratic factor is obtained by dividing
 by (r - 5). Performing the division, we get r^² + 5r + 25. This means that r² + 5r + 25 is the quadratic factor we are looking for.
by (r - 5). Performing the division, we get r^² + 5r + 25. This means that r² + 5r + 25 is the quadratic factor we are looking for.
In summary, the quadratic polynomial that completes the factorization is r² + 5r + 25, and this result is derived from recognizing the given cubic expression as a difference of cubes and factoring accordingly. The quadratic factor is then found by dividing the given cubic expression by the known linear factor (r - 5), resulting in r² + 5r + 25.