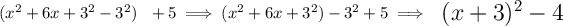Question

Complete the square to transform the expression x^2 + 6x + 5 into the form a(x − h)^2 + k. (1 point)

(x + 3)2 + 4
(x + 6)2 − 4
(x + 3)2 − 4
(x + 6)2 + 4

Answer 1

a perfect square trinomial, namely
`\qquad \textit{perfect square trinomial} \\\\ (a\pm b)^2\implies a^2\pm \stackrel{\stackrel{\text{\small 2}\cdot \sqrt{\textit{\small a}^2}\cdot \sqrt{\textit{\small b}^2}}{\downarrow }}{2ab} + b^2`

where the middle-term is just a product of "2 times the square root of the terms on both sides".

so let's start by grouping the terms with a variable, and then adding the last term for the trinomial, keeping in mind the middle-term is just that product.

`x^2+6x+5\implies (x^2+6x) ~~ +5\implies (x^2+6x+\square^2) ~~ +5 \\\\\\ \stackrel{middle-term}{6x}=2(√(x^2))(√(\square^2))\implies 6x=2x\square\implies \cfrac{6x}{2x}=\square\implies 3=\square`

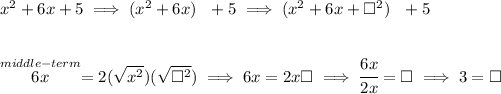
ahhhaaa!!! so our missing term from our group is 3, meaning we need to use 3², however, let's remember, all we're doing is borrowing from our very good friend Mr Zero, 0, so if we add 3², we also have to also subtract 3²

`(x^2+6x+3^2-3^2) ~~ +5\implies (x^2+6x+3^2)-3^2 +5\implies {\Large \begin{array}{llll} (x+3)^2-4 \end{array}}`