The solution to the equation
 .
.
To solve the equation
 , we shall first clarify the equation to ensure we understand the terms correctly:
, we shall first clarify the equation to ensure we understand the terms correctly:
The equation is
 .
.
To solve this equation, we will follow a step-by-step process:
1. **Multiply both sides of the equation by
 ** to eliminate the denominators:
** to eliminate the denominators:
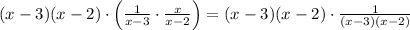
2. Simplify both sides:
On the left side,
 will cancel out one
will cancel out one
 in the numerator, and
in the numerator, and
 will cancel out one
will cancel out one
 in the numerator, leaving us with:
in the numerator, leaving us with:
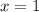
3. We see that once we simplify, what remains is simply
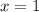 . However, we must be careful to check whether this solution is valid in the context of the original equation.
. However, we must be careful to check whether this solution is valid in the context of the original equation.
4. **Check for extraneous solutions.**
The original equation has denominators that include
 and
and
 . For these denominators to be valid (i.e., we don't divide by zero),
. For these denominators to be valid (i.e., we don't divide by zero),
 cannot be 3 or 2.
cannot be 3 or 2.
Since
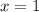 is not equal to 2 or 3, it does not make any denominator zero. Thus, the solution
is not equal to 2 or 3, it does not make any denominator zero. Thus, the solution
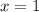 is valid.
is valid.
Therefore, the solution to the equation
 is
is
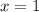 .
.