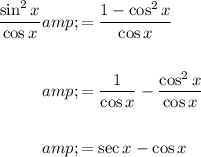Question

Verify that the trigonometric equation is an identity. show all work.

sin^2 x/cos x = sec x - cos x

Answer 1

See below.

Explanation:

Given trigonometric equation:

`(\sin^2 x)/(\cos x)=\sec x- \cos x`

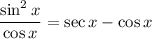
To verify the given trigonometric equation, we can use the following identities:

`\boxed{\begin{array}c\underline{\textsf{Pythagorean identity}}&\underline{\textsf{Reciprocal identity}}\\\\ \sin^2x+\cos^2x=1 & \sec x=(1)/(\cos x)\end{array}}`

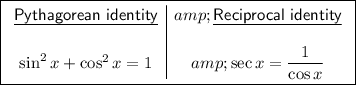
Begin by rewriting the Pythagorean identity to isolate sin²x:

`\sin^2x=1-\cos^2x`

Substitute this into the numerator of sin²x / cos x:

`(\sin^2 x)/(\cos x)=(1-\cos^2 x)/(\cos x)`

`\textsf{Apply the fraction rule:} \quad (a-b)/(c)=(a)/(c)-(b)/(c)`

`=(1)/(\cos x)-(\cos^2x)/(\cos x)`

Use the reciprocal identity for the first fraction, and cancel the common factor cos(x) in the second fraction:

`=\sec x-\cos x`

Hence, the given trigonometric equation has been proved.

`\hrulefill`

As one calculation:

`\begin{aligned}(\sin^2 x)/(\cos x)&=(1-\cos^2 x)/(\cos x)\\\\&=(1)/(\cos x)-(\cos^2x)/(\cos x)\\\\&=\sec x-\cos x\end{aligned}`