A quadratic equation in one unknown;
has two roots. In order to determine these roots, we need to apply certain operations. We can get information about the existence of these roots by discrimination. Below is the discrimination formula.
If we apply discriminant for the above equation, we obtain the following expression;
If the discriminant number is greater than
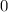 , the equation has two real and distinct roots.
, the equation has two real and distinct roots.
Now let's remember our formula for finding the roots and solve the problem using the discriminant value.
Therefore;
Other root is;