Question

Write an equation for the transformed logarithm shown, that passes through (1,0) and (0,3)

Answer 1

The transformed logarithmic equation that passes through (1,0) and (0,3) is
`\( f(x) = -3 \cdot \log_(10)(2x + 1) + 3 \).`

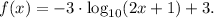
To find the equation for the transformed logarithm, let's consider the general form of a logarithmic function:

`\[ f(x) = a \cdot \log_b(cx + d) + k \]`

where:

-
`\( a \)` is the vertical stretch/compression factor.

-
`\( b \)` is the base of the logarithm.

-
`\( c \)` is the horizontal compression/stretch factor.

-
`\( d \)` is the horizontal shift.

-
`\( k \)` is the vertical shift.

We are given two points that the logarithm passes through:
`\((1, 0)\)` and
`\((0, 3)\).` We can use these points to form a system of equations and solve for the unknowns
`\( a \), \( b \), \( c \), \( d \), and \( k \).`

1. For the point \((1, 0)\):

`\[ 0 = a \cdot \log_b(c \cdot 1 + d) + k \]`

2. For the point \((0, 3)\):

`\[ 3 = a \cdot \log_b(c \cdot 0 + d) + k \]`

Since
`\( \log_b(1) = 0 \)` for any base
`\( b \),` the first equation simplifies to:

`\[ 0 = a \cdot \log_b(d) + k \]`

Now, you have a system of two equations. Solving this system will give you the values of
`\( a \), \( b \), \( c \), \( d \), and \( k \).` Keep in mind that there may be multiple solutions depending on the specific values chosen.