Question

Help with all the steps

Answer 1

Triangle TRS is congruent to QRP by SSS congruence.

To prove that
`$\triangle TRS \cong \triangle QRP$`, we can use the Angle-Bisector Theorem. This theorem states that if a ray bisects an angle of a triangle, then it divides the opposite side into two segments that are proportional to the lengths of the other two sides.

In this case, we are given that
`$\overline{SP}$` bisects
`$\overline{TO}$` and
`$\overline{TO}$` bisects
`$\overline{SP}$`. This means that we have two pairs of proportional segments:

`$(TR)/(TS) = (RP)/(RQ)$` (because
`$\overline{SP}$` bisects
`$\overline{TO}$`)

`$(SP)/(SR) = (PQ)/(PR)$` (because
`$\overline{TO}$` bisects
`$\overline{SP}$`)

We can now use these two proportions to prove that
`$\triangle TRS \cong \triangle QRP$`.

Proof:

1.
`$(TR)/(TS) = (RP)/(RQ)$` (given)

2.
`$(SP)/(SR) = (PQ)/(PR)$` (given)

3. Multiplying both sides of equations 1 and 2, we get:
`$(TR)/(TS) \cdot (SP)/(SR) = (RP)/(RQ) \cdot (PQ)/(PR)$`

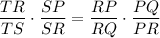
4. Simplifying, we get:
`$(TR \cdot SP)/(TS \cdot SR) = (RP \cdot PQ)/(RQ \cdot PR)$`

5. By the Angle-Bisector Theorem, we know that
`$(TR \cdot SP)/(TS \cdot SR) = (PR \cdot RQ)/(PQ \cdot QR)$`

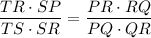
6. Substituting this into equation 4, we get:
`$(PR \cdot RQ)/(PQ \cdot QR) = (RP \cdot PQ)/(RQ \cdot PR)$`

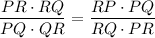
7. Cross-multiplying, we get:
`$PR \cdot RQ \cdot RQ \cdot PR = RP \cdot PQ \cdot PQ \cdot RQ$`

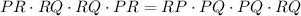
8. Dividing both sides by
`$PR \cdot RQ \cdot PQ$, we get: $PR = RP$`

9. Since PR = RP, we can conclude that
`$\triangle TRS \cong \triangle QRP$` by the Side-Side-Side (SSS) Congruence Theorem.

Conclusion:

We have proven that
`$\triangle TRS \cong \triangle QRP$` using the Angle-Bisector Theorem and the SSS Congruence Theorem.