Question

Please someone help me with this question my exams in a few days

Answer 1

see explanation

Explanation:

(i)

using Pythagoras' identity in the right triangle

the square on the hypotenuse is equal to the sum of the squares on the other 2 sides , that is

(k + x)² = m² + (k - x)² ← expand factors on both sides using FOIL

k² + 2kx + x² = m² + k² - 2kx + x² ( add 2kx to both sides )

k² + 4kx + x² = m² + k² + x² ( subtract k² + x² from both sides )

4kx = m² ( divide both sides by 4k )

x =
`(m^2)/(4k)`

----------------------------------------------------------

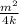
(ii)

the area A of a triangle is calculated as

A =
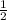`(1)/(2)` bh ( b is the base and h the perpendicular height )

here b = m and h = k - x

A =
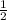`(1)/(2)` m (k - x) ← substitute x =
`(m^2)/(4k)`

=
`(1)/(2)` m ( k -
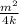
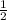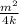`(m^2)/(4k)` ) ← distribute parenthesis

=
`(mk)/(2)` -
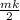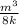`(m^3)/(8k)` ← express as a single fraction

=
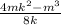`(4mk^2-m^3)/(8k)` ← factor out m from each term in the numerator

=
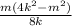`(m(4k^2-m^2))/(8k)` ← factor (4k² - m² ) as a difference of squares

=
`(m(2k+m)(2k-m))/(8k)`