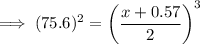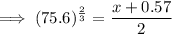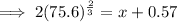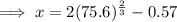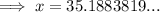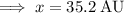Answer:
35.2 AU
Step-by-step explanation:
Kepler's Third Law states that the square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit.

Kepler's Third Law
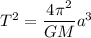
where a is the semi-major axis of the ellipse.
If expressed in the following units:
- T = Earth years.
- a = Astronomical units AU (a=1 AU for Earth).
- M = Solar masses.
then:
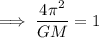
Therefore Kepler's Third Law can be expressed as:
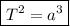
Given:
From inspection of the given diagram:

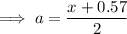
Substitute these values into the equation and solve for x: