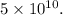Final Answer:
Therefore, the final quotient is
 . In scientific notation, this can be written as
. In scientific notation, this can be written as
 . So, when
. So, when
 is divided by
is divided by
 , the result is
, the result is
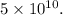
Explanation:
To find the quotient of
 and
and
 , you can simply divide the numerical parts and subtract the exponents:
, you can simply divide the numerical parts and subtract the exponents:
![\[(3 * 10^4)/(6 * 10^(-7)) = (3)/(6) * 10^(4 - (-7)) = (1)/(2) * 10^(11)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1jlkfqw7tvh37o69nlvozvpcawi5aiv3pg.png)
So, the quotient is
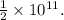
Therefore, the final quotient is
 . In scientific notation, this can be written as
. In scientific notation, this can be written as
 . So, when
. So, when
 is divided by
is divided by
 , the result is
, the result is