Under any circumstances, the imaginary number i = √-1. We use i to represent the square root of a negative number because negative numbers cannot have square roots (ex: 2^2 = 4, -2^2 = 4).
So, we have a complex number 2 + i. The absolue value? Simple.
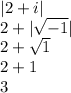
If you need an explanation, look at it this way. The number cannot exist. Yet let's assume it did exist for a moment. What would be the absolute value of a negative square root if they could exist? Well, it would be the same as the square root of that number's opposite, it's positive counterpart!
So, what is the positive counterpart of -1? That would be 1. What's the square root of 1? 1! So, why don't we eliminate these steps? Instead of assuming √-1 can exist and then finding the absolute value of that, just skip those steps and instead take √1, or just 1.
So finally: |√-1| = 1