Question

Select the correct answer. Use the properties of exponents to rewrite this expression. What is the value of the rewritten expression when a = -5?

Answer 1

The correct answer is
`\(\mathbf{B. -500}\)`.

Let's rewrite the expression using the properties of exponents:

`\[ ((2a^4)^2 \cdot a^0 \cdot a^5)/(1) \]`

Now, apply the properties of exponents:

`\[ (2^2 \cdot a^(4 * 2) \cdot a^0 \cdot a^5)/(1) \]`

Simplify the exponents:

`\[ (4 \cdot a^8 \cdot a^0 \cdot a^5)/(1) \]`

`\[ (4 \cdot a^(8+0+5))/(1) \]`

`\[ (4 \cdot a^(13))/(1) \]`

`\[ 4a^(13) \)`

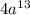
Now, substitute
`\(a = -5\)` into the expression:

`\[ 4(-5)^(13) \]`

Since the base is raised to an odd power and the base is negative, the result will be negative. Calculate:

`\[ 4(-5)^(13) = 4(-1220703125) = -4882812500 \]`

So, the correct answer is
`\(\mathbf{B. -500}\)`.

Complete Question: Select the correct answer. Use the properties of exponents to rewrite this expression.
`frac (2a^4)^2a^0a^5` What is the value of the rewritten expression when a=-5 ?

A -250

B. −500

C. -60

D. -20 Reset Next hentum. All rights reserved.