Question

A large uniform solid disk of mass 175 kg and radius 1.40 m is mounted so that it is horizontal and free to rotate around a vertical axis. A rope is wrapped around the rim of the disk and the disk is made to rotate by pulling on the rope with a constant force of 195 N. If the disk starts from rest, what is its angular speed in rev/s at the end of 2.05 s?

Answer 1

The angular speed of the disk at the end of 2.05 seconds is approximately 3.24 rev/s.

Step-by-step explanation:

In rotational motion problems, the key equation is the rotational analog of Newton's second law, which is τ = Iα, where τ is the torque, I is the moment of inertia, and α is the angular acceleration. In this scenario, the torque (τ) applied by the force F at the edge of the disk can be expressed as τ = rF, where r is the radius. The moment of inertia for a solid disk rotating about its axis is I = (1/2) * m *
`r^2.`

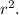
To find the angular acceleration (α), we can use Newton's second law for rotation: τ = Iα. Substituting the expressions for torque and moment of inertia, we get rF = (1/2) * m *
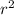`r^2` * α. Solving for α, we find α = (2 * F) / (m * r).

Now, we can use the kinematic equation for rotational motion: ω = ω₀ + αt, where ω is the final angular velocity, ω₀ is the initial angular velocity (which is 0 since the disk starts from rest), α is the angular acceleration, and t is time. Substituting the known values, we get ω = αt = (2 * F * t) / (m * r).

Plugging in the given values (F = 195 N, m = 175 kg, r = 1.40 m, t = 2.05 s), we find ω ≈ (2 * 195 * 2.05) / (175 * 1.40) ≈ 3.24 rev/s. Therefore, the angular speed of the disk at the end of 2.05 seconds is approximately 3.24 rev/s.