Question

The angle of elevation to a nearby tree from a point on the ground is measured to be 69^{\circ}

∘
. How tall is the tree if the point on the ground is 35 feet from the tree? Round your answer to the nearest tenth of a foot if necessary.

Answer 1

The tree is approximately 91.2 ft tall.

Explanation:

Hi there!

We're told:

- angle of elevation = 69 degrees

- there is a point 35 feet from the tree

If we were to draw this out, it would appear to be a right angle triangle. See the picture below.

Now, to solve for the height of the tree, we can use the sine law:

`(a)/( \sin(a) ) = (b)/( \sin(b) )`

where a and b are two sides of a right triangle and A and B are the respective opposite angles

Let the height of the tree = h.

Side h is opposite of the angle measuring 69 degrees:

`\frac{h}{ \sin {69}^(o) }`

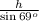
Let the angle opposite of the side measuring 35 feet = A.

`(35)/( \sin(a) )`

Because the sum of a triangle's interior angles is 180 degrees, we know that A=180-90-69=21 degrees.

`\frac{35}{ \sin {21}^(o) }`

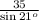
Use the sine law:

`\frac{h}{ \sin {69}^(o) } = \frac{35}{ \sin {21}^(o) }`

`h = \frac{35}{ \sin {21}^(o) } \: \sin {69}^(o)`

`h = 91.17812`

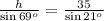
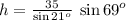
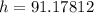
Therefore, the tree is approximately 91.2 ft tall.

I hope this helps!