Question

0=-566° reference angle:
With steps

Answer 1

The coterminal angle of -566° within 0° to 360° is -206°. The original angle is in the third quadrant (180° to 270°), with a reference angle of 26° formed by the terminal side and the nearest x-axis.

To find the coterminal angle, quadrant, and reference angle for the angle
`\(-566^\circ\)`, follow these steps:

1. Coterminal Angle:

- To find a coterminal angle within the range
`\(0^\circ \leq \theta < 360^\circ\)`, you can add or subtract multiples of
`\(360^\circ\).`

-
`\( -566^\circ + 360^\circ = -206^\circ\)`

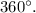
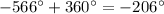
- The coterminal angle within the given range is
`\(-206^\circ\).`

2. Quadrant:

- The original angle
`\(-566^\circ\)` is in the third quadrant.

- Since one full revolution is
`\(360^\circ\)`, each quadrant is
`\(90^\circ\)`, and the third quadrant is from
`\(180^\circ\) to \(270^\circ\).`

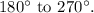
3. Reference Angle:

- The reference angle is the acute angle formed by the terminal side of the angle and the x-axis.

- Since the angle is in the third quadrant, the reference angle is the angle between the terminal side and the nearest x-axis, which is
`\(566^\circ - 540^\circ = 26^\circ\).`

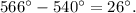
So, for the angle
`\(-566^\circ\):`

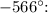
- Coterminal angle:
`\(-206^\circ\)`

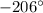
- Quadrant: Third quadrant

- Reference angle:
`\(26^\circ\)`

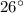
The probable question may be:

For the rotation -566\deg , find the coterminal angle from 0\deg <=\theta <360\deg , the quadrant, and the reference angle.