Question

You are given three pieces of wire that have different shapes (dimensions). You connect each piece of wire separately to a battery. The first piece has a length L and cross-sectional area A. The second is twice as long as the first, but has the same thickness. The third is the same length as the first, but has twice the cross-sectional area. Rank the wires in order of which carries the most current (has the lowest resistance) when connected to batteries with the same voltage difference.

Rank the wires from most current (least resistance) to least current (most resistance).
a. Wire of Lenght L and area A
b. Wire of Lenght 2L and area A
c. Wire of Lenght L and area 2A

Answer 1

The answer is below

Step-by-step explanation:

The resistance of a wire is directly proportional to the length of the wire and inversely proportional to its area. The resistance (R) is given by:

`R=(\rho L)/(A)\\\\where\ L=length \ of\ wire,A=cross\ sectional\ area, \rho=resistivity\ of\ wire.`

Let us assume that all the wires have the same resistivity.

a) Wire of Length L and area A

`R_1=(\rho L)/(A)`

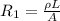
b) Wire of Length 2L and area A

`R_2=(\rho *2L)/(A)=2R_1`

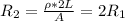
C) Wire of Length L and area 2A

`R_3=(\rho L)/(2A)=(1)/(2)R_1`

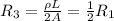
Therefore the wire of least resistance is R3 and R2 has the highest resistivity.

R₃ < R₁ < R₂

Therefore, the ranking of the wires from most current (least resistance) to least current (most resistance) is:

R₃ < R₁ < R₂