Question

How can I solve this question using trigonometry

Answer 1

`(pr)/( \sin(q) ) = (rq)/( \sin(p) ) = (pq)/( \sin(r) )`

Answer 2

a) R = 47.28 R = 312.73 b) 6.67

Explanation:

a)

Use the sine rule to calculate angle PRQ

`(sinQ)/(q) = (sinR)/(r)`

`(sin40)/(7) = (sinR)/(8)`

`0.091827 = (sinR)/(8)`

`sinR = 0.73461`

`sininverse(0.73461) = R`

`R = 47.28`

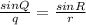
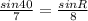
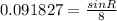
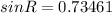
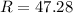
2nd angle for PRQ is 360 - 47.28 = 312.73

b) Use the cosine rule to find side p

p² = r² + q² - 2rqcosP

To find the angle of p we will simply subtract angle R and angle Q from 180.

180 - 47.28 - 40 = 92.72

p² = 8² + 7² + 2(8)(7)cos(92.72)

p² = 107.685

p = √107.685

p = 10.38

Let's suppose that the shortest distance of R from PQ is
`x`.

look at the diagram I gave

since the line I made makes a right angled triangle, we can use SOH CAH TOA

for the angle 40,
`x` is opposite and 10.38 is hypotenuse

which means we will have to use SOH

sin40 = O/H

sin40 =
`x\\`/10.38

0.6428 =
`x`/10.38

0.6428 × 10.38 =
`x`

`x` = 6.67