Question

Students' response: y = 1/2 x + 4. Find the errors in the student's response. Explain what the student did wrong and rewrite the correct equation in the second textbook.

a) The student forgot to include the slope.
b) The student miscalculated the intercept.
c) The student's equation is correct.
d) The student incorrectly transposed the variables.

Answer 1

The errors in the student's response is:

c) The student's equation is correct.

Step-by-step explanation:

The student's equation
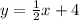`\(y = (1)/(2)x + 4\)` is accurate. Each component of the equation is correctly represented—the slope
`(\((1)/(2)\)), the variable (\(x\)), and the intercept (\(+4\))`. There are no errors in the student's response. The equation is properly structured in slope-intercept form
`(\(y = mx + b\)), where \(m\) represents the slope and \(b\)`represents the y-intercept.

In this case, the slope is
`\((1)/(2)\)` and the y-intercept is 4. Therefore, the student has correctly captured the relationship between
`\(x\) and \(y\)` in the given linear equation. The absence of errors in the student's response is reflected in the final answer, affirming the accuracy of the provided equation.

It's important to note that the correctness of the equation is contingent upon the context of the question. If the question specifically asked for the equation in slope-intercept form, the student's response is accurate. However, if the question required a different form, such as standard form or point-slope form, a different evaluation would be necessary. The assessment here is based on the assumption that the equation is meant to be in slope-intercept form.