The measure of angle R in triangle RST is approximately
 (to the nearest tenth of a degree) using the Law of Cosines.
(to the nearest tenth of a degree) using the Law of Cosines.
To find the measure of angle R in triangle RST , we can use the Law of Cosines, which states that for any triangle with sides a, b, and c and an angle C opposite side c :
![\[ c^2 = a^2 + b^2 - 2ab \cos(C) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/u99md0etz06cy7tevwib3pvagmc7euieif.png)
In this case, r = 4.3 inches, s = 8.9 inches, and t = 6.5 inches. Let's denote R as the angle opposite side r , so c = r . We are solving for angle R :
![\[ 4.3^2 = 8.9^2 + 6.5^2 - 2 \cdot 8.9 \cdot 6.5 \cos(R) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/f6qkbi6bflypy8k79z4dabs12uj5lqe7he.png)
Now, rearrange and solve for cos(R) :
![\[ \cos(R) = (8.9^2 + 6.5^2 - 4.3^2)/(2 \cdot 8.9 \cdot 6.5) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qgs2armivhc3shd9izmu63zux47cf6zgce.png)
Once you find
 ), take the arccosine to find R in radians. Finally, convert radians to degrees. The result is the measure of angle R .
), take the arccosine to find R in radians. Finally, convert radians to degrees. The result is the measure of angle R .
We find that
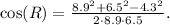
![\[ \cos(R) = (79.21 + 42.25 - 18.49)/(115.7) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8qhid8kg6kdlrx4cg6tt63wwkpyusw5upp.png)
![\[ \cos(R) = (102.97)/(115.7) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/86f5kz9k2mbwzm8o4lxg1fcxmtr05xa4dd.png)
![\[ \cos(R) \approx 0.8897 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/dt8o5fgyyt4q86wu25vzg689l7wromhgix.png)
Now,
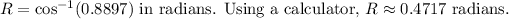
To convert radians to degrees, multiply by

![\[ R \approx 0.4717 * (180)/(\pi) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/7nyuqtgluux9wrd2obcxib68jutnri049l.png)
![\[ R \approx 27.03^\circ \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/flwcre6ghbf6l8n5i6a2ylefu7qn9jcm4r.png)
Therefore, the measure of angle R is approximately
 (to the nearest tenth of a degree).
(to the nearest tenth of a degree).