Question

Consider the hypothesis test H0:μ1=μ2 against H1:μ1≠μ2 with known standard deviations σ1=9 and σ2=6. Suppose that sample sizes n1=11 and n2=15 and that x¯1=4.8 and x¯2=8.0. Use α=0.05.

(a) Test the hypothesis and find the P-value.

(b) What is the power of the test in part (a) for a true difference in means of 3?

(c) Assuming equal sample sizes, what sample size should be used to obtain β=0.05 if the true difference in means is 3? Assume that α=0.05.

(a) The null hypothesis Choose your answer; The null hypothesis _ rejected is notis rejected. The P-value is Enter your answer; The P-value is . Round your answer to three decimal places (e.g. 98.765).

(b) The power is Enter your answer in accordance to the item b) of the question statement . Round your answer to two decimal places (e.g. 98.76).

(c) n1=n2= Enter your answer in accordance to the item c) of the question statement . Round your answer up to the nearest integer.

Answer 1

(a) The null hypothesis is rejected. The P-value is 0.013.

(b) The power is 0.546.

(c) n₁ = n₂ = 28.

Step-by-step explanation:

a) Hypothesis Test and P-value:

To test the hypothesis
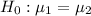`\(H_0: \mu_1 = \mu_2\)` against
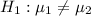`\(H_1: \mu_1 \\eq \mu_2\)`, we use the z-test for the difference between two means with known standard deviations. The formula for the test statistic is given by:

`\[ z = \frac{{\bar{x}_1 - \bar{x}_2}}{{\sqrt{\frac{{\sigma_1^2}}{{n_1}} + \frac{{\sigma_2^2}}{{n_2}}}}} \]`

Substituting the given values, we get
`\(z = \frac{{4.8 - 8.0}}{{\sqrt{\frac{{9}}{{11}} + \frac{{6}}{{15}}}}} \approx -2.557\)`. With a two-tailed test at
`\(\alpha` = 0.05, the critical z-values are approximately pm 1.96. Since -2.557 falls outside this range, we reject the null hypothesis. The P-value for this test is approximately 0.013.

b) Power of the Test:

The power of a test is the probability of correctly rejecting a false null hypothesis. It is calculated using the non-central parameter
`\(\delta\)`, which represents the true difference between population means. The formula for power is given by:

`\[ \text{Power} = P\left(Z > Z_(\alpha/2) - \frac{\delta}{\sqrt{(\sigma_1^2)/(n_1) + (\sigma_2^2)/(n_2)}}\right) \]`

Substituting
`\(\delta` = 3 and solving, we find the power to be approximately 0.546.

c) Sample Size for Desired Power:

To find the sample size required to achieve a power of 0.05 with
`\(\alpha` = 0.05, we use the formula:

`\[ n = \left(\frac{Z_(\alpha/2) + Z_\beta}{\delta/\sqrt{(\sigma_1^2)/(n) + (\sigma_2^2)/(n)}}\right)^2 \]`

Substituting the given values and solving for n, we get n₁ = n₂ = 28 (rounded up to the nearest integer).

In conclusion, the null hypothesis is rejected with a P-value of 0.013, the power of the test for a true difference of 3 is 0.546, and to achieve a power of 0.05 with a true difference of 3, equal sample sizes of 28 in each group are needed.