Question

Suppose that the amount of time WOU students spend on their study is normally distributed with a standard deviation of 2.3 hours. A sample of 80 students is selected at random, and the sample mean obtained is 6.7 hours. (a) Compute the 95% confidence interval estimate of the population mean. (b) Interpret what the interval estimate obtained in (a)

Answer 1

To compute the 95% confidence interval estimate of the population mean, we use the formula: CI = sample mean ± (z * standard deviation / sqrt(sample size)). For a 95% confidence level, the z-score is approximately 1.96. The interval estimate obtained means that we are 95% confident that the true population mean of the amount of time WOU students spend on their study is between 6.0546 and 7.3454 hours.

Step-by-step explanation:

To compute the 95% confidence interval estimate of the population mean, we use the formula:

CI = sample mean ± (z * standard deviation / sqrt(sample size))

where z is the z-score corresponding to the desired confidence level. For a 95% confidence level, the z-score is approximately 1.96.

Plugging in the values, we get:

`CI = 6.7 \± (1.96 * 2.3 / √(80) )`

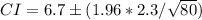
CI = 6.7 ± 0.6454

Therefore, the 95% confidence interval estimate of the population mean is (6.0546, 7.3454).

The interval estimate obtained means that we are 95% confident that the true population mean of the amount of time WOU students spend on their study is between 6.0546 and 7.3454 hours.