Final answer:
A 99% confidence interval for the true proportion of all American adults aged 25 or older with a college degree is computed using the sample proportion of 38.1%, a Z-score for 99% confidence, and the sample size of 814. This interval is unlikely to show that more than half of American adults have a college degree. For a 75% confidence interval with different parameters, further calculations are needed.
Step-by-step explanation:
To construct a 99% confidence interval for the true proportion of all American adults aged 25 or older with a college degree, we start with the given information:
- Sample size (n) = 814
- Sample proportion (p') = 38.1% = 0.381
First, we calculate the point estimate, which is the sample proportion (p'). Then, we need to find the error bound for the confidence interval (EBP). The error bound can be calculated using the following formula:
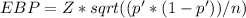
Where Z is the Z-score corresponding to the desired confidence level. For a 99% confidence interval, the Z-score is approximately 2.576.
Let's calculate the EBP:
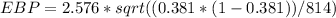
Now, we can compute our confidence interval:
Lower bound = p' - EBP
Upper bound = p' + EBP
After the calculations, if the lower bound of the confidence interval exceeds 50%, we can say (with 99% confidence) that more than half of all American adults have a college degree.
However, since the given point estimate is 38.1%, it is unlikely that the confidence interval would show more than half of all American adults have a college degree.
For part c, using n = 1000 and a point estimate of 38.1%, a 75% confidence interval would require using a different Z-score specific to the 75% confidence level. If the lower bound of this interval is at least 50%, we can conclude (with 75% confidence) that at least half of all American adults believe whatever the poll is addressing.