Question

A random sample of 52 observations was taken. The average in the

sample was 85 with a variance of 400. (Round your answers to three
decimal places.)
(a) Construct a 98% confidence interval for . ?

Answer 1

The 98% confidence interval for the population mean μ is (82.325, 87.675).

Step-by-step explanation:

To compute the confidence interval for the population mean, we can use the formula:

`\[ \bar{x} \pm Z_(\alpha/2) * (\sigma)/(√(n)) \]`

Given the sample average
`(\(\bar{x}\))` is 85, the variance
`(\(\sigma² \))` is 400, and the sample size ((n)) is 52, the standard deviation
`(\(\sigma\))` is
`\(√(400) = 20\).`

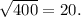
For a 98% confidence interval, the critical value
`\(Z_(\alpha/2)\)` is found using the standard normal distribution. Since it's a two-tailed test, the area in each tail is
`\((1 - 0.98)/(2)` = 0.01). From the z-table or statistical software, (Z_{0.01}) is approximately 2.33.

Plugging the values into the formula:

`\[ 85 \pm 2.33 * (20)/(√(52)) \]`

`\[ 85 \pm 2.33 * (20)/(7.211) \]`

`\[ 85 \pm 2.33 * 2.772 \]`

`\[ 85 \pm 6.454 \]`

Therefore, the confidence interval is (85 - 6.454) to (85 + 6.454), which simplifies to (82.325, 87.675), indicating that we are 98% confident that the population mean falls within this range.