Question

I need help on this sheet is due in a few hours, please help me out!

Answer 1

The roots of the quadratic equations are, respectively:

Case 1: x = 8 or x = - 6, Case 2: x = 0 or x = 2.5, Case 3: x = 1 or x = 7, Case 4: x = - 3, Case 5: x = - 2.5 or x = 2.5, Case 6: x = - 1.333 or x = - 1.5

How to determine the roots of quadratic equation by quadratic formula

Six quadratic equations are found in this exercise, whose roots must be determined by quadratic formula:

`a\cdot x^2 + b\cdot x + c = 0`, where a, b, c are real coefficients.

`x = (- b \pm √(b^2 - 4\cdot a\cdot c))/(2\cdot a)`, where a ≠ 0.

Now we proceed to determine the roots of each quadratic equation:

Case 1: x² - 2 · x - 48 = 0

`x = (2 \pm √(4 - 4\cdot 1\cdot (- 48)))/(2)`

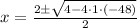
x = 8 or x = - 6

Case 2: 6 · x² - 15 · x = 0

`x = (15\pm √(225 - 4\cdot 6 \cdot 0))/(2\cdot 6)`

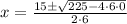
x = 0 or x = 2.5

Case 3: - x² + 8 · x = 7

x² - 8 · x + 7 = 0

`x = (8 \pm √(64 - 4 \cdot 1 \cdot 7))/(2\cdot 1)`

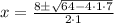
x = 1 or x = 7

Case 4: x² + 4 · x + 17 = 8 - 2 · x

x² + 6 · x + 9 = 0

`x = (- 6 \pm √(36 - 4\cdot 1\cdot 9))/(2\cdot 1)`

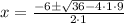
x = - 3

Case 5: 4 · x² - 25 = 0

`x = \pm (√(- 4\cdot 4 \cdot (- 25)))/(2\cdot 4)`

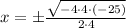
x = - 2.5 or x = 2.5

Case 6: 6 · x² + 18 · x = x - 12

6 · x² + 17 · x + 12 = 0

`x = (- 17 \pm √(17^2 - 4\cdot 6 \cdot 12))/(2\cdot 6)`

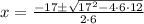
x = - 1.333 or x = - 1.5