Question

Please help need answer now

Answer 1

The slope of AB is (-1–5)/(12-2) = -3/5.
To find the perpendicular bisector, take the negative reciprocal of the slope. The negative reciprocal of -3/5 is 5/3, so the answer is 5/3.

Answer 2

`\sf (5)/(3)`

Explanation:

The slope of the perpendicular bisector of a line segment
`\sf \overline{AB}` is the negative reciprocal of the slope of the line segment
`\sf \overline{AB}`.

The slope of a line passing through two points
`\sf (x_1, y_1)` and
`\sf (x_2, y_2)` is given by:

`\sf m = (y_2 - y_1)/(x_2 - x_1)`

For the line segment
`\sf \overline{AB}`, with points
`\sf A(2,5)` and
`\sf B(12,-1)`:

`\sf m_(AB) = (-1 - 5)/(12 - 2)`

`\sf m_(AB) = (-6)/(10)`

`\sf m_(AB) = -(3)/(5)`

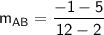
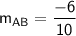
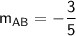
The negative reciprocal of
`\sf -(3)/(5)` is
`\sf (5)/(3)`.

Therefore, the slope of the perpendicular bisector of
`\sf \overline{AB}` is
`\sf (5)/(3)`.