Question

an engineer contributes $350 per month to a retirement account. the account earns interest at a nominal annual interest rate of 6% with interest being credited yearly. what is the value of the account after 40 years?

Answer 1

The retirement account, with $350 monthly contributions at 6% annual interest compounded yearly for 40 years, would reach approximately $28.2 million, assuming consistent contributions and no withdrawals.

To find the value of the retirement account after 40 years, given a monthly contribution of $350 and an annual interest rate of 6% compounded yearly, we can use the formula for the future value of an ordinary annuity:

`\[ FV = P * \left( \frac{{(1 + r)^n - 1}}{r} \right) \]`

Where:

( FV ) = Future Value of the retirement account

( P ) = Monthly contribution ($350)

( r ) = Annual interest rate (6% or 0.06)

( n ) = Number of periods (40 years)

convert the annual interest rate to a monthly interest rate:

`\( r_{\text{monthly}} = \frac{{\text{Annual interest rate}}}{\text{Number of compounding periods per year}} \)`

`\( r_{\text{monthly}} = \frac{{0.06}}{12} = 0.005 \)`

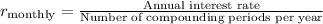
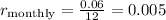
Now, calculate the number of total payments over 40 years:

`\( n = \text{Number of years} * \text{Number of payments per year} \)`

`\( n = 40 * 12 = 480 \)`

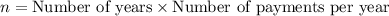
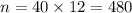
Plug the values into the formula:

`\[ FV = 350 * \left( \frac{{(1 + 0.005)^(480) - 1}}{0.005} \right) \]`

Calculating this yields:

`\[ FV \approx 350 * \left( \frac{{(1.005)^(480) - 1}}{0.005} \right) \]`

`\[ FV \approx 350 * \left( \frac{{404.56052 - 1}}{0.005} \right) \]`

`\[ FV \approx 350 * 80711.0427 \]`

`\[ FV \approx 28,198,866.95 \]`

Therefore, the value of the retirement account after 40 years, considering monthly contributions of $350 and an annual interest rate of 6%, would be approximately $28,198,867.