Question

A rocket is launched from a tower. The height of the rocket, y in feet, is related to the time after launch, x in seconds, by the given equation. Using this equation, find the time that the rocket will hit the ground, to the nearest 100th of second.

y=-16x^2+240x+115

Answer 1

Check the picture below.

so the rocket will hit the ground when y = 0, so hmmm, there's no simple factoring that'd give us integers, so we'll plug the quadratic into the quadratic formula

`~~~~~~~~~~~~\textit{quadratic formula} \\\\ 0=\stackrel{\stackrel{a}{\downarrow }}{-16}x^2\stackrel{\stackrel{b}{\downarrow }}{+240}x\stackrel{\stackrel{c}{\downarrow }}{+115} \qquad \qquad x= \cfrac{ - b \pm \sqrt { b^2 -4 a c}}{2 a} \\\\\\ x= \cfrac{ - (240) \pm \sqrt { (240)^2 -4(-16)(115)}}{2(-16)} \implies x = \cfrac{ -240 \pm \sqrt { 57600 +7360}}{ -32 }`

`x= \cfrac{ -240 \pm \sqrt { 64960 }}{ -32 }\implies x=\cfrac{ -240 \pm 8\sqrt { 1015 }}{ -32 }\implies x=\cfrac{ 240 \mp 8\sqrt { 1015 }}{ 32 } \\\\\\ x=\cfrac{ 30 \mp \sqrt { 1015 }}{ 4 }\implies x\approx \begin{cases} -0.46\\\\ 15.46 ~~ \textit{\large \checkmark} \end{cases}`

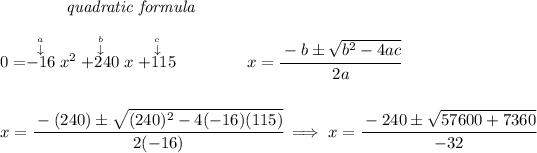
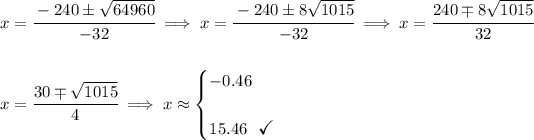
now, let's notice, "x" cannot be negative, so the negative value is tossed.