Question

Integrate (x,y,z)=12xz f ( x , y , z ) = 12 x z over the region in the first octant (x,y,z≥0) ( x , y , z ≥ 0 ) above the parabolic cylinder z=y2 z = y 2 and below the paraboloid z=8−2x2−y2 z = 8 − 2 x 2 − y 2 .

a) 33/2
b) 16/3
c) 8/3
d) 4/3

Answer 1

The integral of
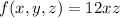`\(f(x, y, z) = 12xz\)` over the specified region in the first octant, above the parabolic cylinder
`\(z = y^2\)` and below the paraboloid \(z =
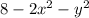`8 - 2x^2 - y^2\)`, evaluates to
`\(16/3\)`. (option b)

Step-by-step explanation:

To solve this triple integral over the given region, it's essential to set up the bounds of integration properly. The region lies in the first octant, where
`\(x\)`,
`\(y\)`, and
`\(z\)` are greater than or equal to 0. The lower boundary is the parabolic cylinder
`\(z = y^2\)` and the upper boundary is the paraboloid
`\(z = 8 - 2x^2 - y^2\)`.

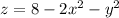Setting up the integral in the order of integration
`\(dz \, dy \, dx\)` over this region involves determining the limits of integration for
`\(z\), \(y\),` and
`\(x\)`. For
`\(z\),` it ranges from
`\(y^2\)` (the lower boundary) to
`\(8 - 2x^2 - y^2\)` (the upper boundary). For
`\(y\)`, it goes from 0 to the curve
`\(y = √(8 - 2x^2)\)`, and for
`\(x\)`, it goes from 0 to \(\sqrt{4}\) to cover the first octant.

Performing the integration in this order yields the value of
`\(16/3\)` (option b) as the result, which represents the integral of
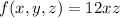`\(f(x, y, z) = 12xz\)` over the specified region.